728x90
다항 시간 알고리즘
" 반복문의 수행 횟수를 입력 크기의 다항식으로 표현할 수 있는 알고리즘 "
알고리즘의 시간 복잡도 분석 (1~3)에서 알아본 알고리즘은 다항 시간이 된다. N^2, N 등 모두 다항 시간 알고리즘이다.
선형 시간이나 선형 이하 시간과는 달리, 다항 시간에 속하는 알고리즘은 엄청나게 큰 시간 차이가 날 수 있다.
N, N^2 뿐만 아니라 N^100 까지도 다항 시간이기 때문이다.
ex) 알러지가 심한 친구들
집들이에 N명의 친구를 초대하려고 한다. 할 줄 아는 M가지의 음식 중 어떤 음식을 대접할 지 고민하는데, 각 친구들은 알러지 때문에 못 먹는 음식들이 많다.
만들 줄 아는 음식의 목록과, 해당 음식을 못먹는 친구들의 목록이 주어졌을 때, 친구들이 먹을 수 있는 음식이 있으려면 최소 몇 가지의 음식을 해야 하는가?
해결 방법
만들어야 하는 음식의 최소 개수를 구해야 하기 때문에, 모든 답을 고려하여야 한다.
- 첫 번째 요리부터 만들지 말지 결정하고, 두 번째 요리를 만들지 말지 결정한다. 이를 모든 요리에 대해 결정한다.
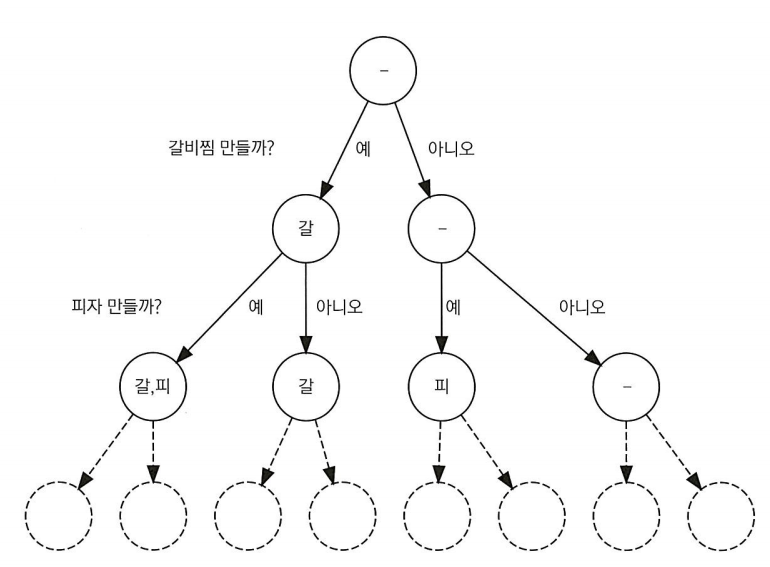
이것을 코드로 구현해보자.
수행 시간
모든 답을 한 번씩 다 확인하기 때문에, 시간은 만들 수 있는 답의 수에 비례하게 된다.
M가지 음식이 있다고 할 때, 모든 경우의 수는 2^M 이다.
답을 하나 만들 때마다 canEverybodyEat()을 수행하므로, 총 수행 시간은 N*M*2^M 이 된다.
지수 시간 알고리즘
위와 같이 N이 하나 증가할 때 마다 걸리는 시간이 배로 증가하는 알고리즘들을 지수 시간에 동작한다고 한다.
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘] 재귀 호출, 재귀 함수란? (0) | 2021.02.08 |
|---|---|
| 알고리즘의 시간 복잡도 분석 - 5. 시간 복잡도 (0) | 2021.01.20 |
| 알고리즘의 시간 복잡도 분석 - 3.선형 이하 시간 알고리즘 (0) | 2021.01.13 |
| 알고리즘의 시간 복잡도 분석 - 2.선형 시간 알고리즘 (0) | 2021.01.11 |
| 알고리즘의 시간 복잡도 분석 - 1.수행 시간 측정 기준 (0) | 2021.01.11 |